
本文代码为java代码
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根节点和两棵互不相交的,分别称为根节点的左子树和右子树的二叉树组成。 --《大话数据结构》
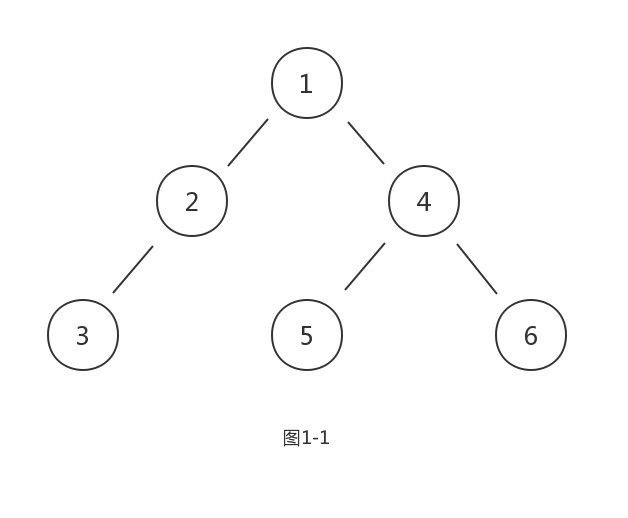
简单的说,二叉树是一种树,并且最多有2个子树。如图1-1:
代码表示:
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x) { val = x; }
}
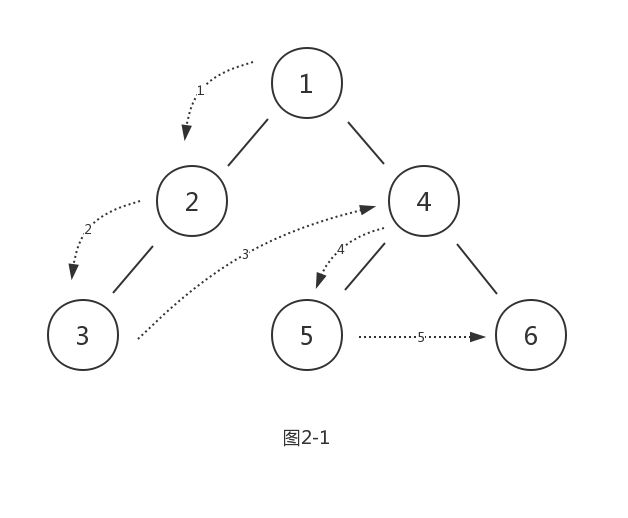
前序遍历的顺序是,根节点->左子树->右子树,遍历子树时也按照相同的顺序,可以用递归的思想理解。遍历顺序如图2-1:
代码表示:
public static void prevPrintTreeNode(TreeNode root){
if(root == null){
return;
}
System.out.print(root.val+" ");
//运用了递归
prevPrintTreeNode(root.left);
prevPrintTreeNode(root.right);
}
所以结果是:{1,2,3,4,5,6}。可知前序遍历结果的第一个节点为根节点。
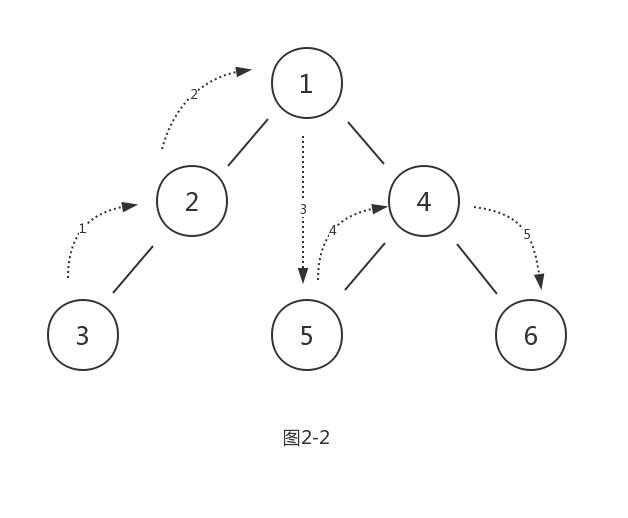
中序遍历的顺序是,左子树->根节点->右子树。遍历顺序如图2-2:
代码表示,只有顺序的区别:
public static void inPrintTreeNode(TreeNode root){
if(root == null){
return;
}
//运用了递归
inPrintTreeNode(root.left);
System.out.print(root.val+" ");
inPrintTreeNode(root.right);
}
所以结果是:{3,2,1,5,4,6}。可知,中序遍历根节点左侧都为左子树节点,右侧都为右子树节点。
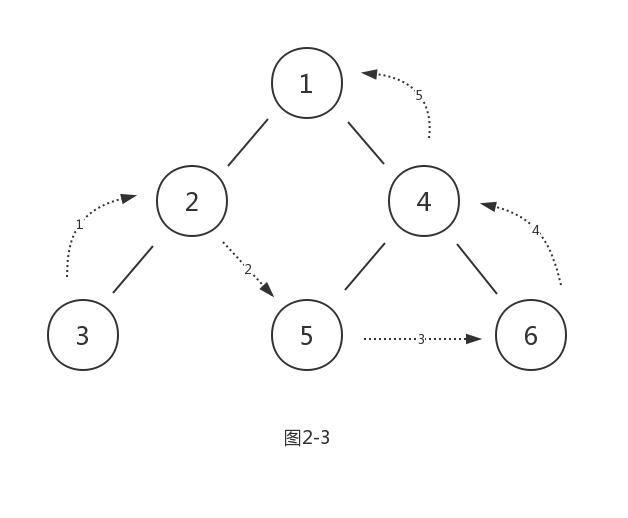
后序遍历的顺序是,左子树->右子树->根节点,遍历顺序如图2-3:
代码表示,依然只有顺序的区别:
public static void postPrintTreeNode(TreeNode root){
if(root == null){
return;
}
//运用了递归
postPrintTreeNode(root.left);
postPrintTreeNode(root.right);
System.out.print(root.val+" ");
}
所以结果是:{3,2,5,6,4,1}。可知,后序遍历最后一个节点是根节点。
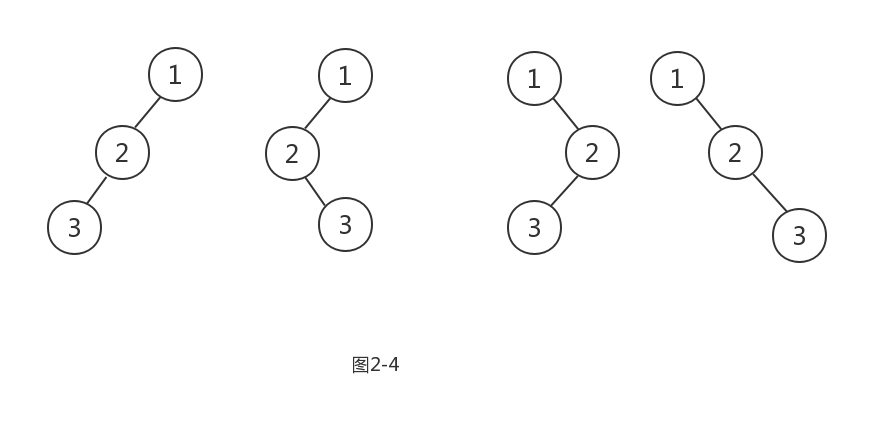
已知前序遍历或后序遍历可以得到根节点,中序遍历在已知根节点的情况下可以得知左子树和右子树的遍历结果,所以已知前序遍历结果和中序遍历结果、已知后序遍历结果和中序比那里结果都可以推导出二叉树结构。但已知前序节点和后序节点不能推导出,因为无法判断左子树和右子树节点个数。比如一个二叉树前序遍历结果为{1,2,3},后序遍历结果为{3,2,1},就有如图2-4的四种可能:
原理第二节讲过了,再画个图便于理解。见图3-1:

合并得到图1-1的二叉树。
代码实现:
public class Solution {
public static TreeNode reConstructBinaryTree(int [] prev,int [] in) {
//不管什么遍历方式,结果长度肯定是一样的,都是总结点数
if(prev.length!= in.length || prev.length<1){
return null;
}
//只有一个节点,那就是根节点
if(prev.length == 1){
return new TreeNode(prev[0]);
}
//在中序遍历结果中找根节点
int index = -1;
for(int i=0;i<in.length;i++){
if(in[i]==prev[0]){
index=i;
break;
}
}
//没找到,说明数据有问题
if(index==-1){
return null;
}
//找到根节点了
TreeNode root = new TreeNode(prev[0]);
//得到左子树的前序遍历结果
int[] lChildPrev = new int[index];
System.arraycopy(prev,1,lChildPrev,0,index);
//得到左子树的中序遍历结果
int[] lChildin = new int[index];
System.arraycopy(in,0,lChildin,0,index);
//通过递归,得到左子树结构
root.left=reConstructBinaryTree(lChildPrev,lChildin);
//得到右子树的前序遍历结果
int[] rChildPrev = new int[in.length-1-index];
System.arraycopy(prev,index+1,rChildPrev,0,in.length-1-index);
//得到右子树的中序遍历结果
int[] rChildin = new int[in.length-1-index];
System.arraycopy(in,index+1,rChildin,0,in.length-1-index);
//通过递归,得到右子树结构
root.right=reConstructBinaryTree(rChildPrev,rChildin);
//得到完整的二叉树结构
return root;
}
//测试
public static void main(String[] args){
int[] prev = {1,2,4,7,3,5,6,8};
int[] in = {4,7,2,1,5,3,8,6};
TreeNode root = reConstructBinaryTree(prev,in);
prevPrintTreeNode(root);
System.out.println();
inPrintTreeNode(root);
}
//测试结果
//1 2 4 7 3 5 6 8
//4 7 2 1 5 3 8 6
}
本文完。